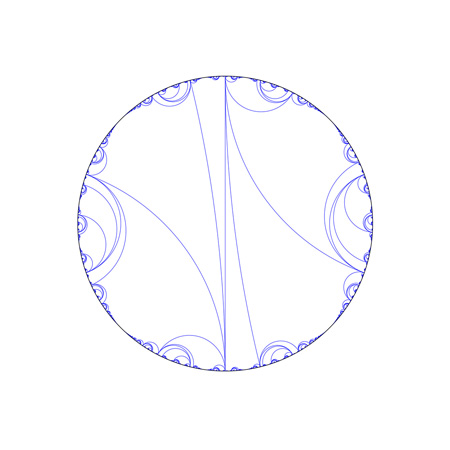
Gallery
Limit Set
Akin to the Julia sets of complex dynamics, the limit set of a Kleinian group depicts the accumulation set of an orbit in hyperbolic space on the ideal boundary at infinity.
Degenerate Group
This limit set is that of a degenerate punctured torus group, one whose action has no finite sided fundamental polyhedron. It arises on the boundary of the deformation space, and is obtained as a limit of the iteration of a pseudo-Anosov action.
Geodesic Lamination
Generalizations of simple closed loops on a surface, geodesic laminations play a key role in understanding asymptotic geometry of hyperbolic spaces. This geodesic lamination on the hyperbolic plane is a lift of a simple one on the punctured torus.
Pleated Surface
A pleated surface in hyperbolic 3-space, this infinitely bent surface is symmetric with respect to the action of a quasi-Fuchsian group – this group arises from the example of a bending deformation (described by W. Thurston in his celebrated lecture notes from Princeton University) called the “Mickey Mouse Example”.